Algorithm Summary
1. What is Breadth-First Search?
Breadth-First Search, or BFS (which is what I will use to refer to this algorithm) provides a quick way to search through an unweighted graph to find the shortest path. It operates in O(E + N) time, where N is the number of nodes in the graph, and where E is the number of connections. However, this algorithm stops working when the distance between nodes are more than a cost of 1.
2. Applications of BFS
BFS can be applied in many different circumstances. It can be used to solve mazes, since the distance between each cell in the maze is always the same (assuming you can only travel in axis-aligned directions). Other applications can be checking whether two nodes are connected to each other, where we don't care about the distance between nodes.
3. How does BFS work?
BFS works by Flood-filling nodes. Lets say we have an initial node N, we can iterate through all of the nodes that are connected to node N, then mark them as visited. For all of the new nodes that we marked as visited, we execute the above procedure, making sure we do not visit any node more than once. One key detail is that the algorithm must ensure that the nodes marked as to be visited should be visited in the order they are marked. This ensures that the distance travelled from the source node(s) to that node is the minimal possible distance.
4. A visual demonstration
Here is our initial graph, we start at node 1, and have it marked as visited. Our target is node 3.
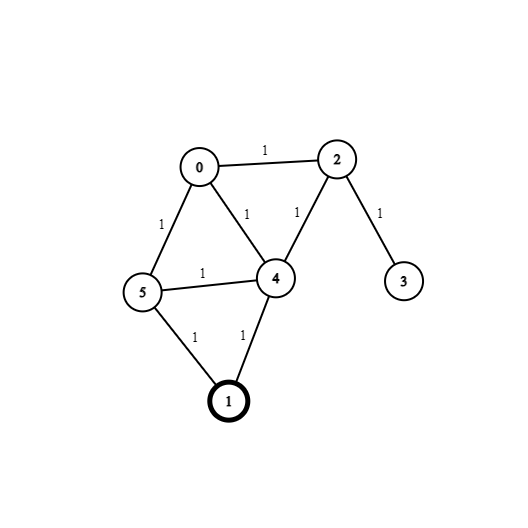
The weights have been set to 1 due to the limitation of the algorithm.
In the second iteration, we have visited two adjacent nodes.
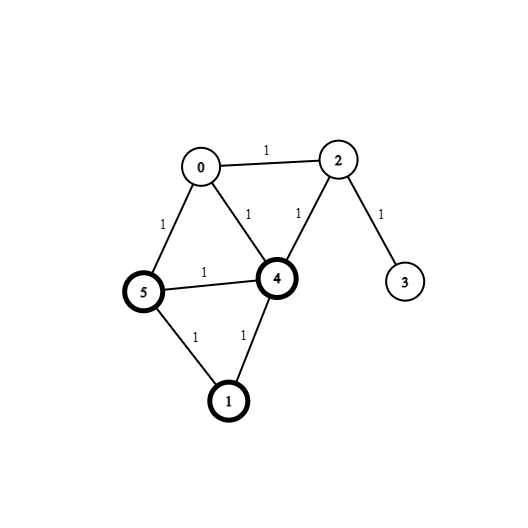
The nodes that are bolded are considered as visited.
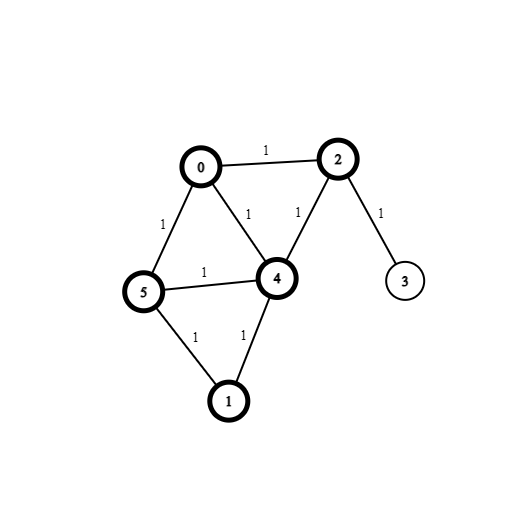
Third iteration:
Finally, we reach our destination in the fourth iteration.
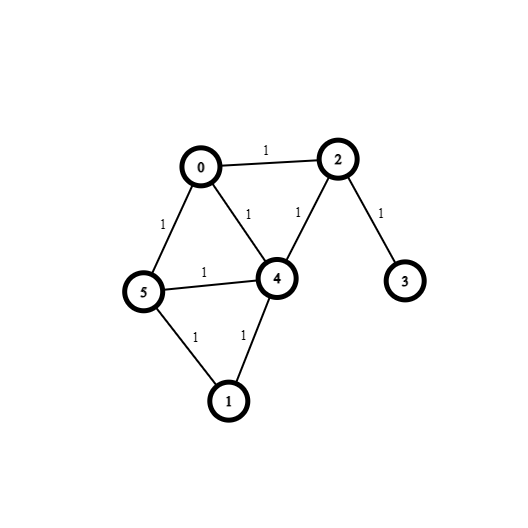
5. A trivial modification
The algorithm shown above cannot (yet) measure the distance between the starting and ending nodes, but a simple modification can be added to track the distance. One such modification can be to simply track the previous node from which the current node was visited. Then, we can count the number of paths the algorithm has traversed through to find the distance.