1. Computers aren't magic.
People tend to believe that computers are super smart. While this may be partially true, Computers are limited to what people can teach it to do. In certain scenarios, for example, we need to find the shortest path between two cities, we need a way to represent the data. This is where graphs come in. Graphs are able to represent connections between distinct nodes. A connection between two hypothetical cities can be stored in an edge, with each city being a node.
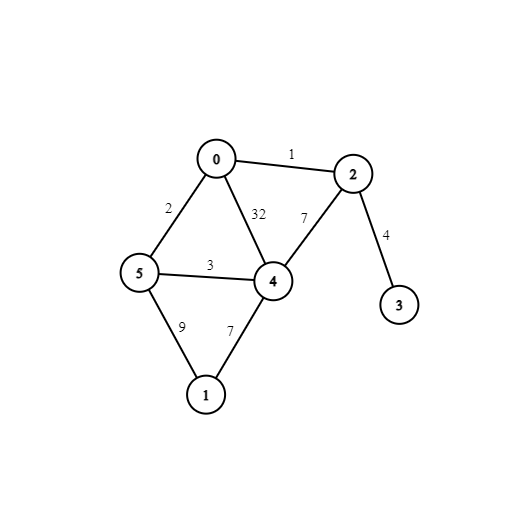
Figure 1. This is a graph. The circles are nodes, and the lines are edges. The numbers on the lines are weights.
2. A step in the right direction.
Now that a computer can understand what these connections are, we need to come up with an algorithm to process the graph. Typical usages for graphs include trying to find the shortest distance between nodes, the minimum edges to connect all nodes, or building dependency graphs. On this website, we will explore the algorithms that can find the shortest path between nodes or cities. Along the way, we will explore the different restrictions that each algorithm has, and the types of problems it can solve.
3. A fork in the path.
This website will cover 3 different algorithms and how they can be applied to solve a problem. For the sake of simplicity, we will ask all 3 of these algorithms what the shortest path from node 1 to node 3 is in the graph on Figure 1.
The algorithms are: